Introduction
I wrote this code to demonstrate how to program artificial intelligence (AI) into a two-player board game after seeing several requests for help on doing so in an online coding forum. I chose tic-tac-toe (also known as noughts and crosses) since virtually everyone knows the game and the rules are simple enough that we don’t need an elaborate analysis of game configurations. Despite being a simple game, the basic AI principles shown here can be applied to more complicated games such as checkers, Connect 4, go and even chess.
So what do we mean programming AI? Basically, we would like a computer player to ‘look’ at a game board and ‘intelligently’ decide where to move. There are of course many ways to do this. In this post we will explore a common method of searching for moves by building game trees that represent the space of possible moves (game configurations) and selecting a move which yields the best outcome.
Game trees can be quite large, particularly so for complex games, and as such can take quite a bit of time to construct and evaluate. Even tic-tac-toe, as simple as it is, has 255,168 possible games if we don’t take symmetries into account (26,830 games when disregarding symmetric games ). That may sound like quite a lot but it pales in comparison to chess which has an estimated 10123 games (now that’s really a lot!). Thankfully, computers are especially suited for dealing with these types of problems though it is interesting to note that for a long time it was believed that a computer would never be able to defeat humans at games like chess. Sadly (or perhaps not) for humans this is no longer the case.
Getting Started
I am going to assume that everyone knows how to play the game so I won’t bother explaining the rules (just in case you don’t read this). If you wish to run the game you will need the .NET 4.0 Framework installed on your machine. If you wish to edit the solution you will need Visual Studio 2010 or Visual Studio Express (I’m pretty sure MonoDevelop works too though I haven’t tested it). The source code for this project can be found here.
In order to follow along, you are going to need some object-oriented programming experience as I assume that the reader understands concepts like using abstract classes and inheritance. The code is written in C# but anyone with java, C++ or VB.NET experience should be okay. The primary focus here will be on the AI portions of the code but I will walk through much of the code. The code shown here are mostly snippets and cannot be copied directly and expected to compile. Use the link above to download the full source code if you wish to tinker with the code.
Creating the Board
We are going to need a game board so let’s start with that code (see snippet below). Internally, the board is modeled as a two-dimensional array of integers. A value of 0 represents an empty space, a value of 1 an ‘X’, and a value of 2 represents an ‘O’. The array indices represent the row and column respectively. Positions on the board are referenced either by specifying the row and column or by specifying a position number. The convention used for position number is shown in figure 1 below. Note that while the internal representation of the board pieces is an int, this is not exposed to clients. Instead an enumeration representing the game pieces is used (enum Pieces) This keeps things clean and prevents coding accidents.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
/// <summary> /// This class represents a tic-tac-toe board /// It is Cloneable so that we can copy board configurations when searching for a next move /// </summary> public class Board : ICloneable { public enum Pieces { X, O, Empty }; int width = 3; int height = 3; protected int[,] board; // a two-dimensional array representing the game board /// <summary> /// Constructs an empty board /// </summary> public Board() { board = new int[ROWS, COLUMNS]; } /// <summary> /// Make a move on the board /// </summary> /// <param name="position">the board position to take</param> /// <param name="piece"></param> public void MakeMove(int position, Pieces piece) { if (!IsValidSquare(position)) throw new InvalidMoveException(); int pieceNumber = GetPieceNumber(piece); Point point = GetPoint(position); board[point.X, point.Y] = pieceNumber; } ... // more code in actual source file } |
You will notice that the Board class implements ICloneable. This is important as our computer player will need to test out moves on Board objects and we don’t want to muck around with the actual game board so we will use clones.
Creating the Tic-Tac-Toe Game
With the board in place we can make the TicTacToe class which models the game itself. It is responsible for keeping track of each player’s turn and making moves on the board and ends the game when a player wins or a draw has been reached. All the logic here is fairly straightforward.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
/// <summary> /// This class represents a Tic-Tac-Toe game board. It includes logic /// to keep track of player turns and assign board squares to a player /// </summary> public class TicTacToeGame { public enum Players { Player1, Player2 }; protected Board board; protected Stack<TicTacToeMove> moves; protected Players currentTurn = Players.Player1; // Player 1 goes first protected bool gameOver = false; /// <summary> /// Constructs a new TicTacToeGame using the default board pieces for player one and two /// </summary> public TicTacToeGame() : this(Board.Pieces.X, Board.Pieces.O) { } /// <summary> /// Constructs a new TicTacToe game using the specified player's pieces. /// /// </summary> /// <param name="player1Piece">Player one's piece</param> /// <param name="player2Piece">Player two's piece</param> public TicTacToeGame(Board.Pieces player1Piece, Board.Pieces player2Piece) { this.player1Piece = player1Piece; this.player2Piece = player2Piece; board = new Board(); moves = new Stack<TicTacToeMove>(); } /// <summary> /// Returns true if the game is over (if there is a winner or there is a draw) /// </summary> /// <returns>true if the game is over or false otherwise</returns> public bool IsGameOver() { return board.IsGameOver(); } /// <summary> /// Undoes the last move /// </summary> public void UndoLastMove() { TicTacToeMove lastMove = moves.Pop(); board.UndoMove(lastMove); SwapTurns(); } /// <summary> /// Returns the player for whose turn it is /// </summary> public Players CurrentPlayerTurn { get { return this.currentTurn; } } /// <summary> /// Makes the move for the specified player /// </summary> /// <param name="m">The move to make</param> /// <param name="p">The player making the move</param> public void MakeMove(TicTacToeMove m, Players p) { if (currentTurn != p) { throw new InvalidMoveException("You went out of turn!"); } if (!board.IsValidSquare(m.Position)) throw new InvalidMoveException("Pick a square on the board!"); board.MakeMove(m.Position, m.Piece); moves.Push(m); SwapTurns(); } ... // more code here } |
When a move is attempted a check is made to ensure that the move is valid and if it is the move is made, otherwise an exception is thrown. The move class is shown below. As you can see it an encapsulation class used to store the move position and piece being moved.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
/// <summary> /// Represents a tic-tac-toe move /// </summary> public class TicTacToeMove { /// <summary> /// Constructs a TicTacToeMove /// </summary> /// <param name="position">The position to move to</param> /// <param name="piece">The piece that is moving</param> public TicTacToeMove(int position, Board.Pieces piece) { this.Position = position; this.Piece = piece; } /// <summary> /// gets or sets the position on the board /// </summary> public int Position { get; set; } /// <summary> /// Gets or sets the piece making this move /// </summary> public Board.Pieces Piece {get; set;} } |
Creating the Players
We will have two kinds of players, human and computer. The human player is responsible for getting a move from a live person while the computer player will search for moves from the game tree it constructs. We will create an abstract Player class to capture the shared properties and functionality of human and computer players. The code for the Player class is shown below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
/// <summary> /// This class abstracts the idea of a Player and includes some commone functionality. /// It includes an event for clients to be notified when a move is made /// </summary> public abstract class Player { // Listen for a move made by a player public event PlayerMovedHandler PlayerMoved; protected TicTacToeMove currentMove; public Player(string name, Board.Pieces p) { this.Name = name; this.PlayerPiece = p; } public abstract void Move(object gameBoard); public TicTacToeMove CurrentMove { get { return currentMove; } } /// <summary> /// This is invoked by subclasses to indicate that the player decided on a move /// </summary> public virtual void OnPlayerMoved() { if (PlayerMoved != null) PlayerMoved(this, new PlayerMovedArgs(currentMove, this)); } /// <summary> /// Get or Set the player's piece /// </summary> public Board.Pieces PlayerPiece { get; set; } /// <summary> /// Get or set the player's name /// </summary> public string Name { get; set; } } |
You will notice that the Player class includes the event PlayerMoved. This is used to notify listeners when a move has been made. This is useful because the move selection for the players run in their own thread so that it does not block the main thread (and UI) while waiting for a player to select a move.
The code for HumanPlayer is shown below. All it does is wait for a click on the game board UI and then invokes the PlayerMoved event which is handled by the game TicTacToeForm class (see source code).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
/// <summary> /// This class represents a Human Player /// </summary> public class HumanPlayer : Player { protected TicTacToeForm ticTacToeForm; protected bool alreadyMoved = false; public HumanPlayer(string name, Board.Pieces p, TicTacToeForm tttf) : base(name, p) { this.ticTacToeForm = tttf; } /// <summary> /// Make a move. Waits for the player to double click a square /// and then triggers the PlayerMoved Event /// </summary> /// <param name="gameBoard"></param> public override void Move(object gameBoard) { // start listening to clicks ticTacToeForm.SquareDoubleClicked += new SquareDoubleClickHandler(SquareDoubleClicked); // now wait until the user clicks while (!alreadyMoved) ; // reset the flag alreadyMoved = false; // raise the PlayerMovedEvent OnPlayerMoved(); } // when a user double clicks a square on the TicTacToeForm this method receives the // event message // the current move is set and the alreadyMoved flag is set to true so that the // which breaks the while loop in the Move method void SquareDoubleClicked(object sender, TicTacToeBoardClickedEventArgs args) { // unregister the double clicked event ticTacToeForm.SquareDoubleClicked -= SquareDoubleClicked; currentMove = new TicTacToeMove(args.BoardPosition, this.PlayerPiece); alreadyMoved = true; } } |
Computer Player
Now we are getting to the interesting part — getting the computer to make an ‘intelligent’ move. In order to accomplish this we are going to need some way of placing a value on how good a given move is. For this purpose we will define an evaluation function, e(m), that the computer player will use to see how favorable a particular move m, is. We will follow usual convention and choose e(m) to be large if a move is likely to result in a win and small if it is likely to result in a loss. With the evaluation function in place we can use the minimax algorithm to select a move that maximizes e(m). We will take a closer look at the minimax algorithm in a bit but for now let’s define the evaluation function.
Defining an Evaluation Function
There are many ways to construct an evaluation function that meets our criteria. The way I chose is fairly simple: for each row, column and diagonal on the board, count the number of the players pieces (an ‘X’ or an ‘O’) that are present if it is possible for a win in that row, column or diagonal and subtract that from that value we get from the same evaluation for the opponent’s piece. Kind of a mouthful, I know. Have a look at figure 2 below which shows a sample calculation of e(m) with ‘X’ next to move.
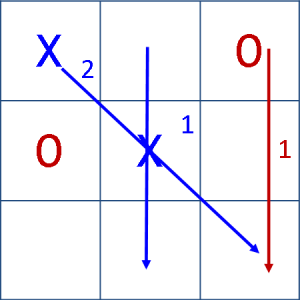
Figure 2: For ‘X’, two pieces in the diagonal = 2
1 ‘X’ in second column = 1
For ‘O’, the ‘O’ in the third column = 1
e(m) = 3 – 1 = 2
This configuration is favorable to ‘X’
NOTE: There are certainly other ways to define the evaluation function for tic-tac-toe and you may wish to experiment doing that.
It is convenient to define a very large value for e(m) when a configuration represents a win for ‘X’ and a very small value when there is a loss for ‘X’. We are free to choose any sufficiently large number as long as we can guarantee that it is impossible for non-winning configurations to yield the same e(m). Conceptually, I like to use ±∞. In this program I used double.MaxValue and double.MinValue respectively. The evaluation function there has definite upper and lower bounds. We are certain that -10 ≤ e(m) ≤ 10 so there is no danger of approaching double.MaxValue or double.MinValue in a non-winning configuration.
Note: The .NET framework has an implementation of infinity (double.PositiveInfinity and double.NegativeInfinity), that would also work, I just happened to not use it.
Side Note: I would like to stress that it is extremely important to have an evaluation function that accurately estimates the ‘goodness’ or ‘badness’ of a position. This is not so difficult for tic-tac-toe because there is not much strategy to consider and we won’t need to look too far ahead to see whether we have chosen a good move or not. A game like chess however, is a completely different matter. A poor evaluation function will lead to a very bad computer player even in end-game scenarios where there are only a few moves to make. In more complex games, you may need to experiment a bit with fine-tuning the evaluation function to ensure that it reasonably characterizes how favorable a given configuration is.
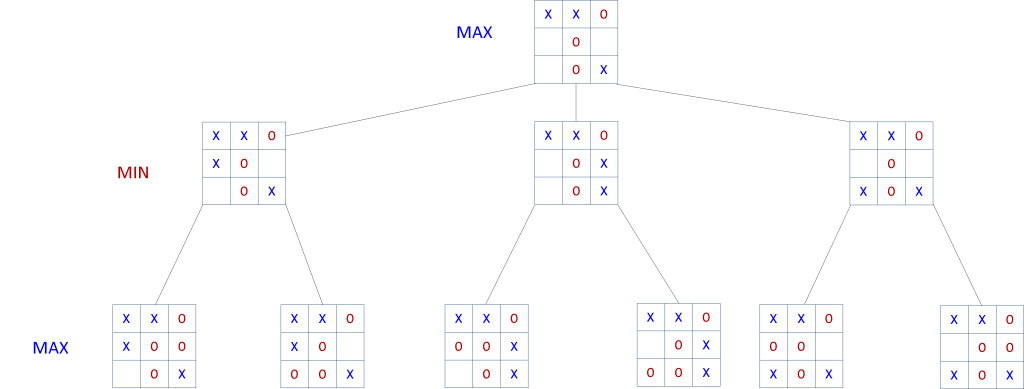
Now that we have an evaluation function we are ready to describe the minimax algorithm (informally), which will enable our computer player to decide on an ‘intelligent’ move. What we will do is make a tree of possible moves down to a given depth. The depth represents how many levels of moves the computer will look ahead. A tree of depth of 2 contains all the possible moves the computer can make and all of the subsequent moves that the computer’s opponent can counter with. The tree’s root node will represent the initial board configuration. We will have two kinds of nodes, MAX nodes and MIN nodes. MAX node are used to represent configurations for which the computer must move and MIN nodes represent board configurations for which the computer’s opponent must move. Thus, the tree’s root node is always a MAX node. MAX nodes select the move that results in the MAXimum e(m) value from its children.
The children of the root node will represent configurations of all the possible moves that the computer can make. These nodes are MIN nodes because they represent game configurations for which ‘O’ (the opponent) will move and as such they will select moves that MINimize e(m) values. We continue construction of the tree by generating children for these MIN nodes, which are of course MAX nodes since it will be the computer’s turn again in the board configurations represented. The tree construction continues in this manner until we reach the specified depth.
Let’s walk through an example using the configuration in figure 3 shown below. It is the computer’s move who is ‘X’ and we are going to create a tree of depth of 2.

Figure 3: It is ‘X’s move. This configuration will be represented by the root node of our game tree.
This will be our root node, and since it represents a configuration for which the computer needs to move it is a MAX node. The computer can move in positions 3, 5, and 6. Each of the moves yield a new configuration and are represented as children of the root node. Because the child nodes represent configurations for which the opponent must move they are MIN nodes (see figure 4 below).
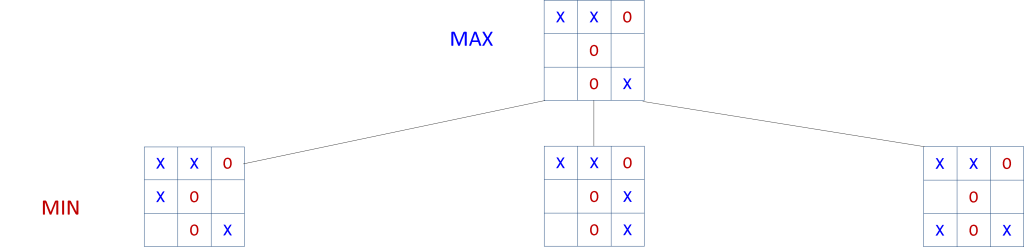
Figure 4: Game tree showing three children spawned from the root node representing an ‘X’ move to position 3, 5, and 6 respectively
We need to make another set of children for each of the min nodes to achieve the desired depth of 2. Since these children are the children of MIN nodes they will be MAX nodes. This is always the case. MAX nodes have MIN children and vice-versa. The graphic below shows the complete tree for depth 2.
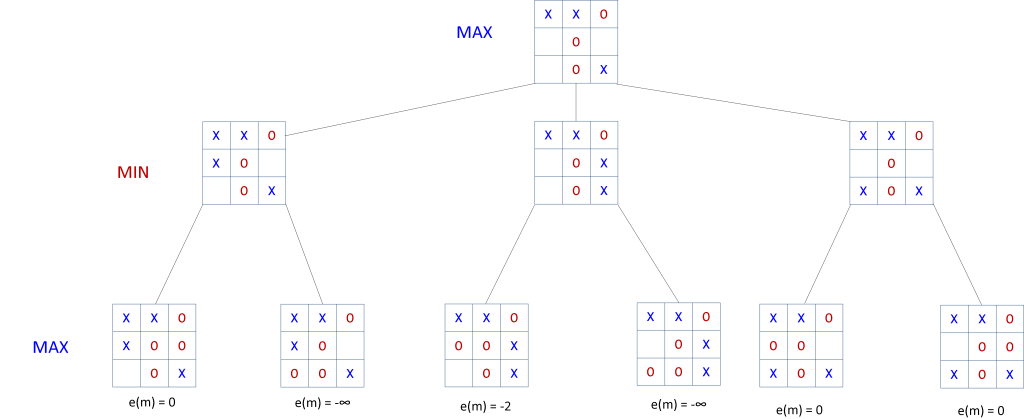
We can now begin to apply the minimax algorithm. We do this bottom up. Figure 5 below shows the tree with the e(m) values calculated by the evaluation function for the bottom child nodes.
With the e(m) values calculated for the bottom children each of the MIN nodes can select their best move. The best move for a MIN node is the child node that has the minimum value since that represents the best configuration for ‘O’. The image below shows the tree after the MIN nodes have been assigned the values of their best child nodes. The values the MIN nodes have selected are shown circled to the right of the min nodes. These are displayed this way to distinguish selected values from values that are calculated directly from the evaluation function. Only nodes on the bottom level use the evaluation function to compute their values.
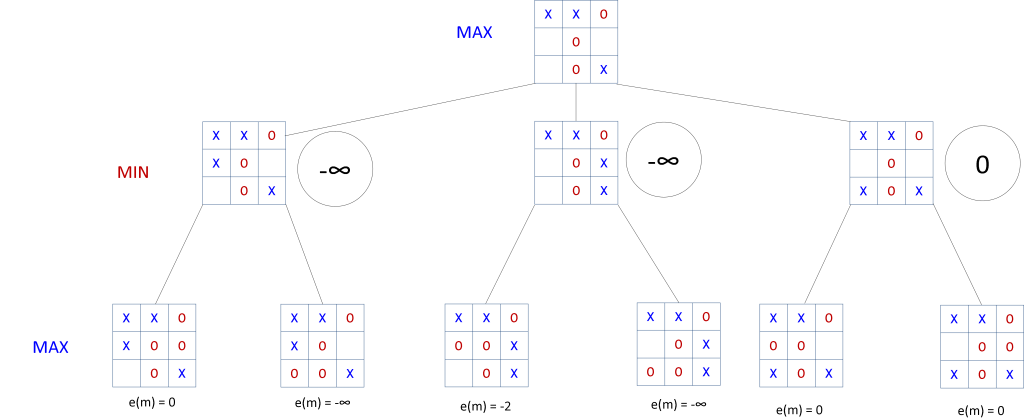
Figure 7: The MIN nodes are assigned the values representing their best move, which is the child node that has the minimum e(m) value.
Now the root node selects the maximum value from among it’s children. The node with e(m)= 0 is the maximum so that is selected by the root node as the best move for the computer to make (moving to position 6). The algorithm predicts a loss if a move to position 3 or 5 is made where e(m) = -∞ for those moves.
The code below implements the evaluation function that was described earlier.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 |
/// <summary> /// This class represents a static evaluation function for Tic-Tac-Toe /// The value is computed by summing number of game pieces in the rows, columns, and diagonals /// for those rows, columns and diagonals that are still winnable /// </summary> public class EvaluationFunction { public EvaluationFunction() { } /// <summary> /// Evaluates the favorability of the current board configuration for maxPiece. Higher values /// indicate better configuration for maxPiece /// </summary> /// <param name="b">the game board to evaluate</param> /// <param name="maxPiece">the piece representing MAX</param> /// <returns></returns> public double Evaluate(Board b, Board.Pieces maxPiece) { if (b.HasWinner()) { if (b.WinningPiece == maxPiece) return double.MaxValue; else return double.MinValue; } double maxValue = EvaluatePiece(b, maxPiece); double minValue = EvaluatePiece(b, Board.GetOponentPiece(maxPiece)); return maxValue - minValue; } // sums up all the possible ways to win for the specified board piece private double EvaluatePiece(Board b, Board.Pieces p) { return EvaluateRows(b, p) + EvaluateColumns(b, p) + EvaluateDiagonals(b, p); } // over all rows sums the number of pieces in the row if // the specified piece can still win in that row i.e. the row // does not contain an opponent's piece private double EvaluateRows(Board b, Board.Pieces p) { int cols = b.Columns; int rows = b.Rows; double score = 0.0; int count; // check the rows for (int i = 0; i < b.Rows; i++) { count = 0; bool rowClean = true; for (int j = 0; j < b.Columns; j++) { Board.Pieces boardPiece = b.GetPieceAtPoint(i, j); if (boardPiece == p) count++; else if (boardPiece == Board.GetOponentPiece(p)) { rowClean = false; break; } } // if we get here then the row is clean (an open row) if (rowClean && count != 0) score += count; } return score; } // over all rows sums the number of pieces in the row if // the specified piece can still win in that row i.e. the row // does not contain an opponent's piece private double EvaluateColumns(Board b, Board.Pieces p) { int cols = b.Columns; int rows = b.Rows; double score = 0.0; int count; // check the rows for (int j = 0; j < b.Columns; j++) { count = 0; bool rowClean = true; for (int i = 0; i < b.Columns; i++) { Board.Pieces boardPiece = b.GetPieceAtPoint(i, j); if (boardPiece == p) count++; else if (boardPiece == Board.GetOponentPiece(p)) { rowClean = false; break; } } // if we get here then the row is clean (an open row) if (rowClean && count != 0) score += count; //Math.Pow(count, count); } return score; } // over both diagonals sums the number of pieces in the diagonal if // the specified piece can still win in that diagonal i.e. the diagonal // does not contain an opponent's piece private double EvaluateDiagonals(Board b, Board.Pieces p) { // go down and to the right diagonal first int count = 0; bool diagonalClean = true; double score = 0.0; for (int i = 0; i < b.Columns; i++) { Board.Pieces boardPiece = b.GetPieceAtPoint(i, i); if (boardPiece == p) count++; if (boardPiece == Board.GetOponentPiece(p)) { diagonalClean = false; break; } } if (diagonalClean && count > 0) score += count;// Math.Pow(count, count); // now try the other way int row = 0; int col = 2; count = 0; diagonalClean = true; while (row < b.Rows && col >= 0) { Board.Pieces boardPiece = b.GetPieceAtPoint(row, col); if (boardPiece == p) count++; if (boardPiece == Board.GetOponentPiece(p)) { diagonalClean = false; break; } row++; col--; } if (count > 0 && diagonalClean) score += count; return score; } } |
Implementing MINIMAX
Like the HumanPlayer class our ComputerPlayer class will extend Player and need to implement the Move method. We will build our search tree using Node objects that will represent a particular move made. As discussed earlier, there are two types of Nodes, MAX and MIN nodes. In code, we define the MaxNode and MinNode classes that will represent MAX and MIN nodes respectively. We will make use of an abstract Node class to capture the common properties and functionality of MIN and MAX nodes. The code for the Node class is shown below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 |
/// <summary> /// This class represents a Node in the search Tree. /// Each Node contains a particular board configuration. Nodes 0 or more children /// that represent subsequent moves from that Node's board. /// /// </summary> public abstract class Node { // this nodes children protected List<Node> children; // the value associated with the node -- this is the result of the // evaluatio function for leaf nodes protected double value; // The child node that represents the best move // for a node. protected Node bestMoveNode; // the board that this node represents protected Board board; // the evaluation function protected static EvaluationFunction evaluator; protected Board.Pieces myPiece; // the piece representing the node's piece protected Board.Pieces opponentPiece; // the opponents piece // the move that was made from the parent node that created this node TicTacToeMove move; Node parent = null; /// <summary> /// Constructs a new Node /// </summary> /// <param name="b">The board that the Node will use to evaluate itself and generate its children</param> /// <param name="parent">The parent of this node</param> /// <param name="move">The move from the parent's board that generated this node's board</param> public Node(Board b, Node parent, TicTacToeMove move) { this.board = b; this.parent = parent; this.move = move; if (parent != null) myPiece = Board.GetOponentPiece(parent.MyPiece); children = new List<Node>(); } /// <summary> /// The game piece that this node 'has' /// </summary> public Board.Pieces MyPiece { get { return myPiece; } set { myPiece = value; opponentPiece = Board.GetOponentPiece(value); } } /// <summary> /// sets the evaluation function used by this node to calculate /// its value /// </summary> public EvaluationFunction Evaluator { set { evaluator = value; } } /// <summary> /// The value of this node either computed by the evaluation function /// or the value selected from among child nodes, /// </summary> public double Value { get { return value; } set { this.value = value;} } /// <summary> /// /// </summary> public abstract void Evaluate(); /// <summary> /// Selects the best move node for the node /// </summary> public void SelectBestMove() { // if no children there is no best move for the node if (children.Count == 0) { bestMoveNode = null; return; } // sort the children so that the first element contains the 'best' node List<Node> sortedChildren = SortChildren(this.children); this.bestMoveNode = sortedChildren[0]; Value = bestMoveNode.Value; } /// <summary> /// Finds the best move for the node. /// </summary> /// <param name="depth">The depth to search</param> public virtual void FindBestMove(int depth) { if (depth > 0) { // expand this node -- subclasses provide their own implementation of this GenerateChildren(); // evaluate each child // if there is a winner there is no need to go further down // the tree // sends the Evaluate() message to each child node, which is implemented // by subclasses EvaluateChildren(); // check for a winner bool haveWinningChild = children.Exists(c => c.IsGameEndingNode()); if (haveWinningChild) { // the best move depends on the subclass SelectBestMove(); return; } else { foreach (Node child in children) { child.FindBestMove(depth - 1); } SelectBestMove(); } } } /// <summary> /// Checks to see if the node is either a winner or MAX or MIN /// </summary> /// <returns>true if either 'X' or 'O'</returns> public virtual bool IsGameEndingNode() { return Value == double.MaxValue || Value == double.MinValue; } /// <summary> /// The best move from this node's board configuration /// </summary> public TicTacToeMove BestMove { get { return this.bestMoveNode.move; } } // create the children protected void GenerateChildren(); // evaluate the child nodes protected void EvaluateChildren() { foreach (Node child in this.children) { child.Evaluate(); } } protected abstract List<Node> SortChildren(List<Node> unsortedChildren); // does the node's configuration represent a winner // for the node in question protected abstract bool IsWinningNode(); } |
All Node objects have a parent (with the exception of the root node of course) and zero or more children. Each Node has a value associated with it, either computed directly from the evaluation function or by selecting the maximum (for MAX Nodes) or minimum (for MIN Nodes) value of the children. The Node class also keeps track the move made to its parents board to generate its own board. There is also the BestMove property which enables a node to keep track of its best move. The FindBestMove method defined in the Node class constructs the game tree and drives the search for a best move. Don’t worry about the details now as we will see later how this all works when we do an example.
Let’s take a look at the MaxNode and MinNode classes:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
/// <summary> /// This class represents a MAX node in the game tree. /// </summary> public class MaxNode : Node { /// <summary> /// Constructs a new max node /// </summary> /// <param name="b">The Board that this node represents</param> /// <param name="parent">The node's parent</param> /// <param name="m">The move made to create this node's board</param> public MaxNode(Board b, Node parent, TicTacToeMove m) : base(b, parent, m) { } // Generate Children. MAX Nodes have MIN children protected override void GenerateChildren() { // create child nodes for each of the availble positions int[] openPositions = board.OpenPositions; foreach (int i in openPositions) { Board b = (Board) board.Clone(); TicTacToeMove m = new TicTacToeMove(i, myPiece); b.MakeMove(i, myPiece); children.Add(new MinNode(b, this, m)); } } // Evaluates how favorable the board configuration is for this node protected override void Evaluate() { this.Value = evaluator.Evaluate(this.board, myPiece); } // does this node have a winning game configuration protected override bool IsWinningNode() { return this.Value == double.MaxValue; } // returns a List of this nodes children sorted in descending order protected override List<Node> SortChildren(List<Node> unsortedChildren) { List<Node> sortedChildren = unsortedChildren.OrderByDescending(n=> n.Value).ToList(); return sortedChildren; } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
/// <summary> /// This class represents a MIN node in the game tree /// </summary> public class MinNode : Node { /// <summary> /// Constructs a MIN node /// </summary> /// <param name="b">The board that this node represents</param> /// <param name="parent">This node's parent</param> /// <param name="m">The move that was made from the parent to lead to this node's board</param> public MinNode(Board b, Node parent, TicTacToeMove m) :base(b, parent, m) { } // Generates the node's children. MIN nodes have MAX children protected override void GenerateChildren() { int[] openPositions = board.OpenPositions; foreach (int i in openPositions) { Board b = (Board)board.Clone(); TicTacToeMove m = new TicTacToeMove(i, myPiece); b.MakeMove(i, myPiece); children.Add(new MaxNode(b, this, m)); } } // determines if this node is a winner // by convention a winning node for a MIN node // is double.MinValue protected override bool IsWinningNode() { return this.value == double.MinValue; } // returns a list of the child nodes in ascending order // the first node in the list will be the best node for the min node protected override List<Node> SortChildren(List<Node> unsortedChildren) { List<Node> sortedChildren = unsortedChildren.OrderBy(n => n.Value).ToList(); return sortedChildren; } /// <summary> /// evalutes the value of the node using the evaluation function /// </summary> protected override void Evaluate() { Value = evaluator.Evaluate(board, Board.GetOponentPiece(myPiece)); } } |
You can see that the abstract Node class implements the search in the FindBestMove method while the concrete MaxNode and MinNode add some node-specific operations like sorting and creating children.
Now that we can create the game trees and select best moves we are ready to implement the ComputerPlayer class. The code for ComputerPlayer is shown below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
/// <summary> /// This class represents a "comuter" player. /// It determines moves using minmax decision rules /// </summary> public class ComputerPlayer : Player { public const int DEFAULT_SEARCH_DEPTH = 3; /// <summary> /// Constructs a new computer player. The DEFAULT_SEARCH_DEPTH is used /// </summary> /// <param name="name">The name of the player</param> /// <param name="p">The piece this player is using in the came</param> public ComputerPlayer(string name, Board.Pieces p) : this(name, p, DEFAULT_SEARCH_DEPTH) { } /// <summary> /// Constructs a new computer player /// </summary> /// <param name="name">The name of the player</param> /// <param name="p">The piece the player is using</param> /// <param name="searchDepth">The depth to search for moves in the game tree.</param> public ComputerPlayer(string name, Board.Pieces p, int searchDepth) :base(name, p) { this.SearchDepth = searchDepth; } /// <summary> /// gets or sets the search depth which is the number of moves /// the computer player will look ahead to determine it's move /// Greater values yield better computer play /// </summary> public int SearchDepth { get; set; } /// <summary> /// Start the computer searching for a move /// Clients should listen to the OnPlayerMoved event to be notified /// when the computer has found a move /// </summary> /// <param name="gameBoard">The current game board</param> public override void Move(object gameBoard) { Board b = (Board)gameBoard; Node root = new MaxNode(b, null, null); root.MyPiece = this.PlayerPiece; root.Evaluator = new EvaluationFunction(); root.FindBestMove(DEFAULT_SEARCH_DEPTH); currentMove = root.BestMove; OnPlayerMoved(); } ... } |
Like HumanPlayer, the search for a move begins when an instance of ComputerPlayer is sent the Move message. To get the ball rolling, the ComputerPlayer creates the root node of the tree (a MaxNode), which is given a reference to the current game board (well actually it is a clone of the current board — we do not want to mess up the actual game board). The evaluation function is set and the root node’s FindBestMove (recall that this is implemented in the abstract Node class) method is invoked with the default search depth of 3.
The first thing done in FindBestMove is to check that depth > 0. Since this is the first pass and depth = 3, it enters the if block and the GenerateChildren method is invoked and a child node is created for each empty position in the root node’s Board representing all the possible initial moves that the computer can make . Each of these children will be MinNodes since their parent is a MaxNode.
After the GenerateChildren method is called the EvaluateChildren method is invoked, which causes the child nodes to computer their Value via the evaluation function. Strictly speaking, the algorithm we described does not call for evaluating the nodes at this point. According to the algorithm, we are only required to evaluate nodes at depth 3 or any terminal nodes (nodes for which there is a completely full board or a board in which one player has won). I’ll go into a little more detail later as to why I chose to evaluate the children now, but for the sake of this example, let us assume that we do not find any winning nodes until we at least complete our tree.
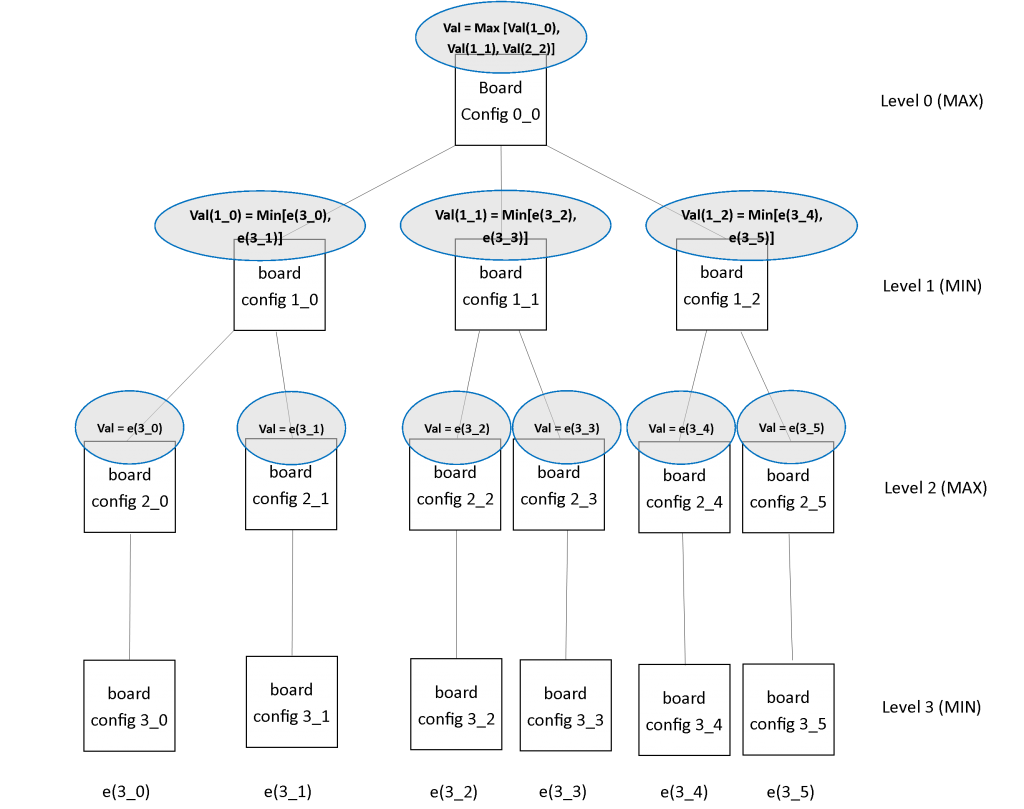
Now we use a bit of recursion and for each child that the root node has that node’s FindBestMove method is invoked passing along a depth of 2. Child nodes are again created, level 2 nodes, which are are MaxNodes since they are the immediate descendants of the MinNodes from level 1. Again a recursive call to FindBestMove is invoked on each of the children this time with a depth of 1. For the last time, children are made, which are MinNodes, and the recursive call to FindBestMove is made with a depth of 0. This time, depth > 0 is false so FindBestMove simply returns doing nothing and control is returned to the foreach block which puts us back to the first level 2 Node (node 2_0). Then SelectBestMove method is invoked on that node. Since the level 2 nodes are MaxNodes, the SelectBestMove method defined in MaxNode is used to select the maximum e(m) value from among its children. Control then returns to the parent of the first level 2 Node (node 1_0) we created. The series of illustrations below show how a tree of depth 3 is generated in the FindBestMove method.
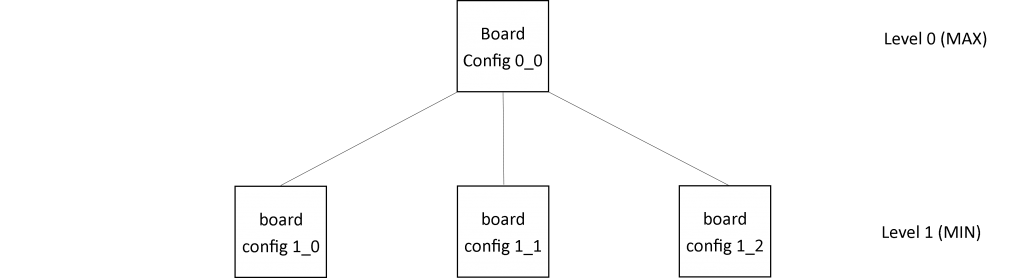
Figure 8(a): Tree state after the first call to the FindBestMove method and after GenerateChildren is invoked but before first recursive call to FindBestMove
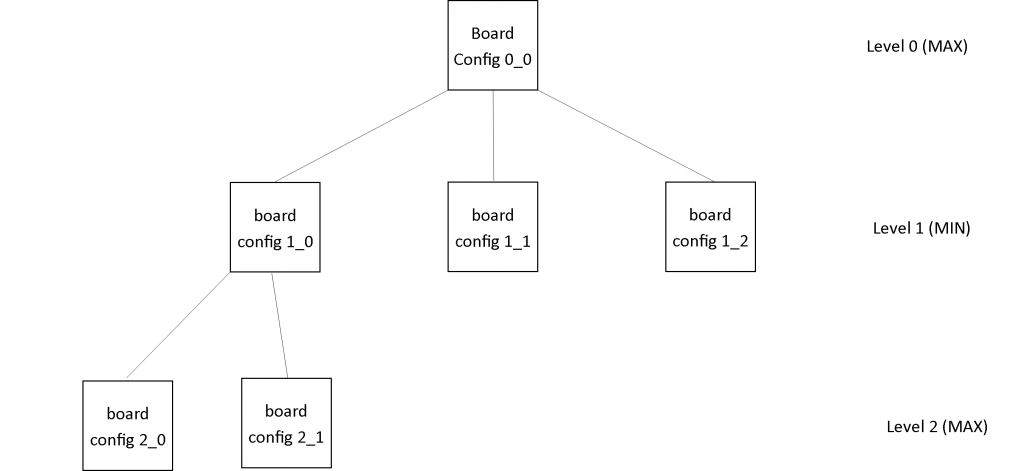
Figure 8(b): Tree state after first recursive call to FindBestMove with depth = 2 from the 1_0 node, after the GenerateChildren Method has been invoked but before the recursive call to FindBestMove again
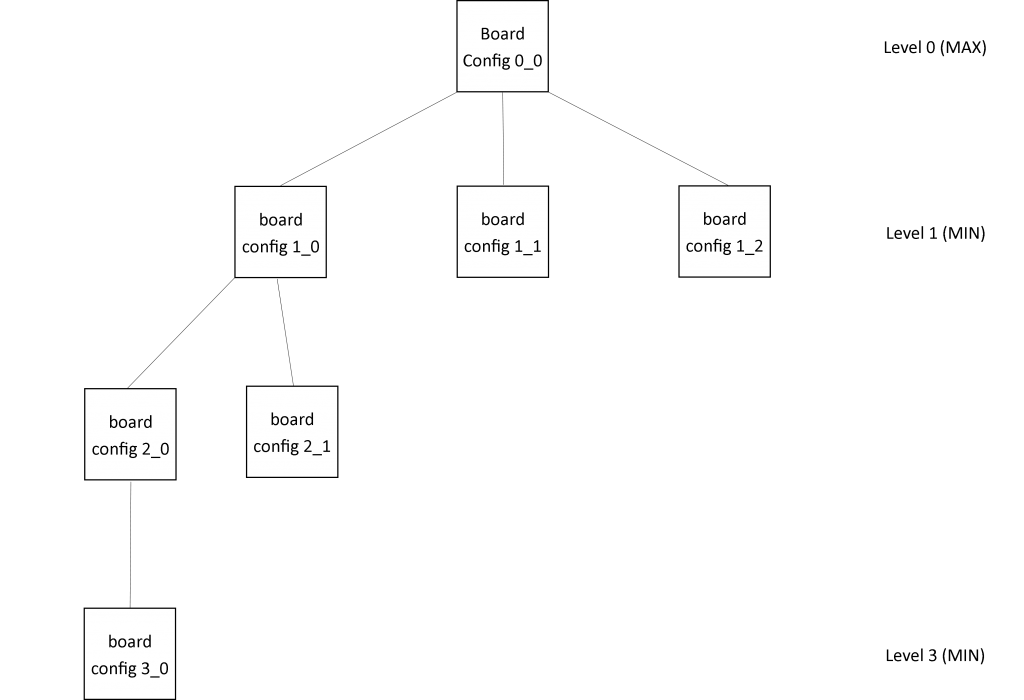
Figure 8(c): Tree state after second recursive call to FindBestMove with depth = 1 from the 2_0 node after the GenerateChildren method is invoked but before subsequent recursive call to FindBestMove. The call to FindBestMove with depth = 0 from node 3_0 is then made but returns doing nothing. The SelectBestMove is invoked and node 2_0 sets it’s value to the max value of its children (the value of its only child, node 3_0).
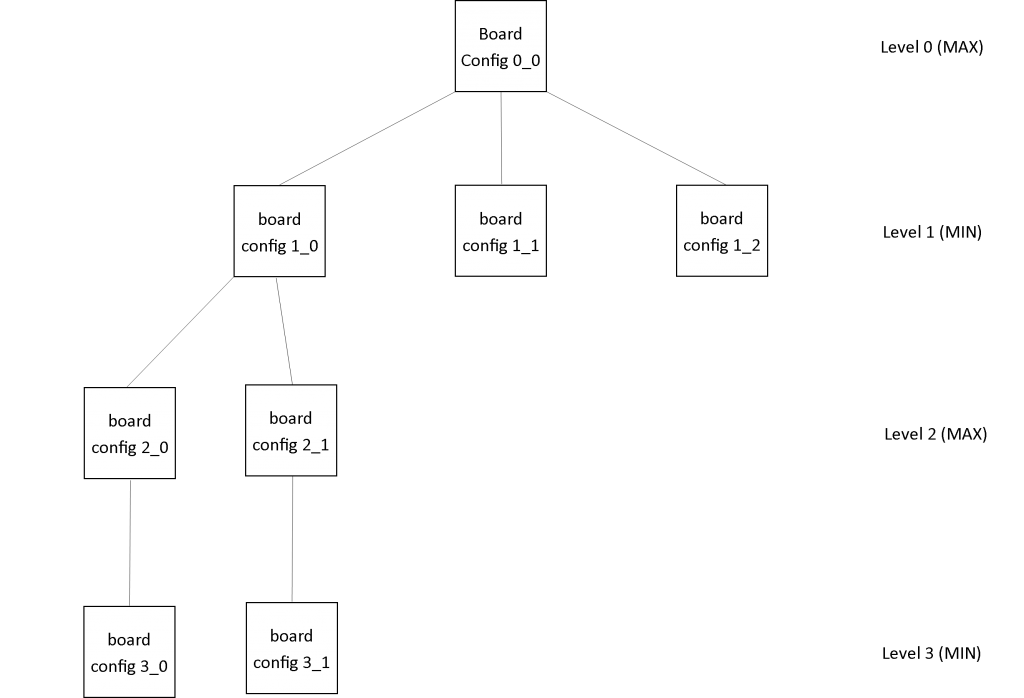
Figure 8(d): Tree state after recursive call to FindBestMove with depth = 1 from the 2_1 node after the GenerateChildren method is invoked but before subsequent recursive call to FindBestMove. The call to FindBestMove with depth = 0 from node 3_1 is then made but returns doing nothing. The SelectBestMove is invoked and node 2_1 sets it’s value to the max value of its children (the value of its only child, node 3_1).
After the tree state in figure 8(d), FindBestMove is invoked on node 1_1 and proceeds in the same manner as shown in steps (b) through (d) above but on node 1_1. Likewise, FindBestMove is invoked on node 1_2 and the tree is completed and the root node selects the maximum value from among the Level 1 children. The illustration below shows the final tree.
Now that we walked through the find best move method I want to explain why I decided to generate all the children and evaluate them first rather than proceeding one child at a time (a depth-first traversal). This is done in case we find that one of the children represents a move that wins the game and as such we need not proceed any further, since that node will be selected as best from its parent no matter what the other child nodes yield (we might do the same but no better). Not only does this prevent us from generating the tree unnecessarily, it also ensures we select the shortest path to victory. For example, let’s say we have the configuration shown below and it is X’s turn (the computer).
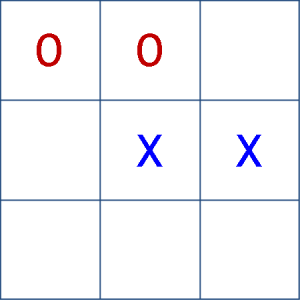
Figure 9: This configuration could lead the computer selecting to block ‘O’ in position 2 rather than move to position 3 and win the game.
Obviously the computer should move to position 3 and win the game. However, with minimax it is possible that the computer selects to move to position 2 and block ‘O’ from winning. But why? Notice that if ‘X’ blocks ‘O’ at position 2, this also guarantees ‘X’ a win as that move gives ‘X’ two ways of winning, one across the diagonal and another in the third column. So no, matter what ‘O’ does next ‘X’ still wins. As far as the standard minimax algorithm is concerned these two moves are equally favorable. All it cares about is winning. There isn’t any mechanism to select for shorter paths to victory. With the check for a winning node that we do in FindBestMove, we eliminate this from happening. This is good practice for two reasons. First, it cuts down the number of computations required by reducing the tree size (none of the winning nodes siblings will have children generated for them), which can be significant when the game is more complicated than tic-tac-toe. Second, if we have a less than perfect evaluation function that doesn’t accurately estimate the favorability, we may actually end up losing by selecting a move in which we expect to win several moves down the line.
Creating Players and Running the Game
So now that we have an ‘intelligent’ computer player capable of making its own moves let’s set up a game. In the Program class (see Program.cs) we create our players and run the game. The code snippet below shows how to create a human Vs computer match. As far as I can tell the computer player is impossible to beat even when the search depth is 3. We aren’t limited to human vs computer games. You could also have human vs human (not fun) or you could reenact Wargames and set two computer players against one another.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
static class Program { /// <summary> /// The main entry point for the application. /// </summary> [STAThread] static void Main() { Application.EnableVisualStyles(); Application.SetCompatibleTextRenderingDefault(false); TicTacToeForm f = new TicTacToeForm(); // Create the game players // Players can be either human or computer players // It does not matter which piece 'X' or 'O' player 1 or two have // but they must be different // Create a human player Player p1 = new HumanPlayer("Joe", Board.Pieces.X, f); // Create a computer player // You can create varying degrees of difficulty by creating computer // players that build bigger game trees // uncomment desired player and comment all other player 2s // create a computer player with the default game tree search depth Player p2 = new ComputerPlayer("HAL", Board.Pieces.O); // Create a computer player that only looks ahead 1 move // i.e only considers their immediate move and not any subsequent moves // by their opponent. // this is a very poor player // Player p2 = new ComputerPlayer(Board.Pieces.X, f, 1); // Creates an advanced computer player that looks ahead 5 moves // Player p2 = new ComputerPlayer("Advanced HAL", Board.Pieces.X, 5); f.AddPlayer(p1); f.AddPlayer(p2); Application.Run(f); } } |
Final Thoughts
I hope that some of you found some things of interest in this post. Let me know if there are any questions or comments. I love getting feedback. For anyone who wants to take this code to the next level I would suggest looking at the following:
- Try and define a different evaluation, maybe you could come up with a better one than I presented here.
- Look into alpha-beta pruning. This describes a method of ‘pruning’ the tree to reduce the tree size and allow the computer to look ahead further in a shorter amount of time. Again, not really required for tic-tac-toe but it will most certainly return dividends in more complex games.
- Try coding AI for a harder game like Connect 4. In order to use the game tree ideas presented here in a more complicated game, you can use the code in the Node classes as is but you must change the evaluation function and add support for your own game board. Of course, you would probably want to implement alpha-beta pruning as well.
- For the more adventurous, you could try and make a ComputerPlayer class that uses a neural network to select moves and in fact ‘learn’ (you will need to train this type of player with a given set of examples or from manually playing against it many times) from experience rather than using a static evaluation function.


Thank you for the long explanation. It helps me for doing my own artificial intelligence in my 3 in a row university’s work.
maybe are some languages mistakes, sorry, i’m still learning english.
Thank you!
Thanks!
Thank you!